SIFAT-SIFAT FUNGSI (fungsi Surjektif, Into, Injektif, Bijektif)
1. Fungsi Surjektif
Fungsi f : A → B disebut fungsi surjektif (fungsi onto atau fungsi kepada) jika setiap elemen di B mempunyai pasangan di A atau Rf = B, atau untuk setiap y ∊ B terhadap x ∊ A sedemikian sehingga f(x) = y.
2. Funsi Into
Fungsi f : A → B disebut fungsi into (fungsi ke dalam) jika terdapat elemen B yang tidak mempunyai pasangan atau prapeta di A.
3. Fungsi Injektif
Fungsi f : A → B disebut fungsi injektif (fungsi satu-satu) jika setiap elemen dari B mempunyai pasangan tepat satu elemen dari A. Dengan perkataan lain:
- Fungsi f : A → B dikatakan fungsi injektif jika untuk setiap x1, x2 ∊ A dan x1 ≠ x2, maka f(x1) ≠ f(x2)
- Fungsi f : A → B dikatakan fungsi injektif jika untuk setiap x1, x2 ∊ A dan f(x1) = f(x2) maka x1 = x2.
4. Fungsi Injektif
Fungsi f : A → B disebut fungsi bijektif, jika f adalah fungsi injektif dan sekaligus fungsi surjektif. Oleh karena itu, himpunan A dan B dikatakan berkorespondensi satu-satu.
Pembahasan Soal tentang sifat-sifat fungsi
Soal 1
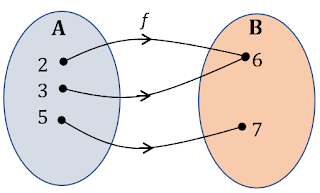
Diberikan himpunan A = {2,3,5} dan B = (6,7). Jika f : A → B dengan f = {(2,6); (3,6); (5,7), apakah fungsi f adalah fungsi surjektif?
Jawab:
Fungsi f = {(2,6); (3,6); (5,7), dapat disajikan dalam diagram panah. Karena Rf = B, maka fungsi f adalah fungsi surjektif.
Periksalah apakah fungsi f(x) = 2x – 4 adalah fungsi surjektif?
Jawab:
Fungsi f merupakan fungsi surjektif karena untuk setiap y ∊ R kodomain x ∊ R domain. Misalkan y = 2x – 4 atau ½ (y + 4), sehingga
f(x) = f[½(y + 4)]
f(x) = 2[½(y + 4)] – 4
f(x) = y
Range dari fungsi f sama dengan kodomainnya.
Soal 3
Diberikan himpunan A = {0, 1, 2} dan B = {4, 5, 6}. Fungsi f = {(0, 4); (1, 5); (2, 5)}. Nyatakan fungsi f dalam diagram panah dengan f : A à B. Fungsi apakah fungsi f?
Jawab:
Fungsi f adalah fungsi into, sebab terdapat elemen B, yaitu 6 yang tidak mempunyai prapeta di A.
Soal 4
Diberikan fungsi f(x) = x2. Tentukan domain fungsi f agar fungsi f merupakan merupakan fungsi injektif.
Jawab:
Df = {x | x ≤ 0, x ∊ R}, seperti gambar (i) atau
Df = {x | x ≥ 0, x ∊ R}, seperti gambar (ii)
1. Domain, Range, dan Kodomain Fungsi
5. Fungsi Ganjil & Fungsi Genap
7. Sifat-Sifat Fungsi (Sifat Surjektif, Into, Injektif, Bijektif)
9. Pengertian Komposisi Fungsi
10. Syarat Agar Dua Fungsi dapat Dikomposisikan
11. Komposisi Dua Fungsi atau Lebih
13. Sifat-Sifat Komposisi Fungsi
14. Pengertian Invers Suatu Fungsi
15. Menentukan Invers Suatu Fungsi
16. Sifat Grafik Fungsi Invers
17. Menentukan Fungsi f Jika Fungsi g dan g ○ f atau f ○ g Diketahui dengan Menggunakan Invers Fungsi
){kind=link}
Post a Comment for "SIFAT-SIFAT FUNGSI (fungsi Surjektif, Into, Injektif, Bijektif)"
Sobat Ayo Sekolah Matematika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!