Di sini kita akan membahas tentang konsep dasar Teorema Faktor.
Jika polinomial p(x) dibagi dengan x - α maka dengan algoritma pembagian,
P (x) = (x - α) q(x) + S,
di mana q(x) adalah hasil bagi dan S adalah sisa yang merupakan konstanta.
Menempatkan x = α di P(x) = (x - α) q(x) + S, kita dapatkan,
p(α) = (α - α) q(α) + S
⟹ p(α) = S.
Jika R = p(α) = 0, maka
p(x) = (x - α) q(x) dan sebagainya (x - α) adalah faktor dari p (x).
x - α merupakan faktor dari p(x) jika p(α) = 0, dan jika p(α) = 0 maka p(x) memiliki faktor x - α.
Contoh Teorema Faktor:
Buktikan bahwa x + 5 adalah faktor dari 2x2 + 7x - 15. Sekarang, x + 5 = x - (-5) dan
p (-5) = 2(-5)2 + 7(-5) - 15
= 50 - 35 - 15
= 0.
Jadi, x - (-5), yaitu x + 5 adalah faktor dari 2x2 + 7x - 15
Kesimpulan: ax + b merupakan faktor dari p(x) jika p (-b/a) = 0, dan jika p(-b/a) = 0 maka p(x) memiliki faktor x - α.
Di sini kita akan membahas tentang penerapan Teorema Faktor.
Contoh 1. Cari akar persamaan 2x2 - 7x + 6 = 0. Maka faktorkanlah 2x2 - 7x + 6.
Jawab:
Di sini, persamaannya adalah 2x2 - 7x + 6 = 0
⟹ 2x2 - 4x - 3x + 6 = 0
⟹ 2x(x - 2) - 3(x - 2) = 0
⟹ (x - 2)(2x - 3) = 0
⟹ x - 2 = 0 atau 2x - 3 = 0
⟹ x = 2 atau x = 3/2
Oleh karena itu, 2x2 - 7x + 6 = 2(x - 2)(x – 3/2) = (x - 2)(2x - 3)
Contoh 2. Tentukan persamaan kuadrat yang berakar 1 + √3 dan 1 - √3.
Jawab:
Kita tahu bahwa persamaan kuadrat yang berakar α dan β adalah
(x - α) (x - β) = 0
Oleh karena itu, persamaan yang dibutuhkan adalah {x - (1 + √3)} {x - (1 - √3)} = 0
⟹ x2 - {1 - √3 + 1 + √3}x + (1 + √3)(1 - √3) = 0
⟹ x2 - 2x + (1 - 3) = 0
⟹ x2 - 2x - 2 = 0.
Contoh 3. Tentukan persamaan kubik yang berakar 2, √3 dan -√3.
Jawab:
Kita tahu bahwa persamaan kuadrat yang berakar dari α, β dan γ adalah
(x - α)(x - β)(x - γ) = 0
Oleh karena itu, persamaan yang dibutuhkan adalah (x - 2)(x - √3){x - (-√3)} = 0
⟹ (x - 2)(x - √3)(x + √3) = 0
⟹ (x - 2)(x2 - 3) = 0
⟹ x3 - 2x2 - 3x + 6 = 0.
⟹ x2 - {1 - √3 + 1 + √3} x + (1 + √3)(1 - √3) = 0
⟹ x2 - 2x + (1 - 3) = 0
⟹ x2 - 2x - 2 = 0.
Contoh 4. Faktorkan x2 -3x - 9
Jawab:
Persamaan yang sesuai adalah x2 - 3x - 9 = 0
Sekarang kami menerapkan rumus kuadrat
Maka,
FAKTRORISASI:
☺Persamaan Polinomial dan Akarnya
☺Contoh Soal pada Teorema Sisa danPembahasannya

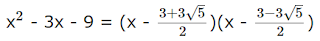
Post a Comment for "Teorema Faktor"
Sobat Ayo Sekolah Matematika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!