Soal dan Pembahasan Himpunan

Soal 1: UTBK SBMPTN 2019  

Daerah yang diarsir menyatakan himpunan...
(A) $(A\cap B)\cup (A\cap C)$
(B) $(A\cup B)\cap (A\cap C)$
(C) $(A\cup B)\cap (A\cup C)$
(D) $(A\cup C)\cap (B\cup C)$
(E) $(B- A)\cup (C-A)$

Soal 2: UMPTN 1997 Rayon B 
Jika $K \subset L$, $L \subset M$ dan $K'$ adalah komplemen $K$, maka $(M-L)\cup (L-K)'=...$
(A) $M\cap L' \cap K$
(B) $M\cap (L \cup K)$
(C) $M\cap (L' \cup K')$
(D) $L\cup K'$
(E) $L'\cup K$

PEMBAHASAN:
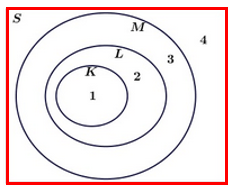
Kita menggunakan bantuan diagram Venn sederhana di bawah ini

Dari diagram venn di atas kita peroleh {$K = 1$}, {$L=1,2$}, {$M=1,2,3$} dan {$S=1,2,3,4$}

• Pernyataan pilihan $\left(A\right)$

         $M\cap L' \cap K=$ {$1,2,3$} $\cap$ {$3,4$} $\cap$ {$1$}
         $M\cap L' \cap K=$ {$1$} 

• Pernyataan pilihan $\left(B\right)$

        $M\cap (L \cup K)=$ {$1,2,3$} $\cap$ ({$3,4$} $\cup$ {$1$})
        $M\cap (L \cup K)=$ {$1,2$}  

• Pernyataan pilihan $\left(C\right)$

        $M\cap (L' \cup K')=$ {$1,2,3$} $\cap$ {$3,4$} $\cup$ {$2,3,4$}
        $M\cap (L' \cup K')=$ {$2,3$} 

• Pernyataan pilihan $\left(D\right)$

        $L\cup K'=$ {$1,2$} $\cup$ {$2,3,4$}
        $L\cup K'=$ {$1,2,4$} 

• Pernyataan pilihan $\left(E\right)$

        $L'\cup K=$ {$1,3,4$} $\cup$ {$1$}
        $L'\cup K=$ {$1,3,4$} 

• Dari pernyataan soal 

        $(M-L)\cup (L-K)'=$ {$3$} $\cup$ {$1,3,4$}
        $(M-L)\cup (L-K)'=$ {$1,3,4$} 

Jadi $(M-L)\cup (L-K)' \equiv L'\cup K$

Pilihan yang sesuai adalah $\left(E\right)$

Soal 3: UTBK SBMPTN 2019  

Daerah yang diarsir menyatakan himpunan...
(A) $A\cup (B \cap C)$
(B) $(A\cup B)\cap C$
(C) $A\cap (B \cup C)$
(D) $(A\cap B) \cup C$
(E) $A - (B \cap C)$ 

Soal 4: UMPTN '97 
Jika himpunan semesat $S=$ {${1,2,3,4,5,6,7,8,9}$}, $A=$ {${1,3,5}$}, $B=$ {${2,4,6,8}$} dan $B'$ komplemen $B$, maka $B'-A=...$

(A) {$\phi$}
(B) {${9}$}
(C) {${7,9}$}
(D) {${1,3,5,7,9}$}
(E) {${2,4,6,8,9}$}

PEMBAHASAN:
Dengan diagram Venn berikut, kita peroleh,

• $B'$ anggota-anggotanya adalah $S$ (semesta) yang bukan anggota $B$. Jadi, $B'=$ {$1,3,5,7,9$}
• $(B'-A)$ anggota-anggotanya adalah $B'$ yang bukan anggota $A$. Jadi $(B'-A)=$ {$7,9$}

Pilihan jawabannya adalah (C)

Soal 5: UMPTN 1993 Rayon C 
Jika $A^c$ adalah komplemen $A$, maka daerah yang diarsir pada diagram Venn di samping dapat dinyatakan dengan . . . .

(A) $P\cap Q \cap R^c$
(B) $(R\cap Q)^c \cap P)$
(C) $P^c \cup R^c \cup Q$
(D) $P\cup (R^c \cap Q))$
(E) $(P \cup R^c) \cap Q^c$

PEMBAHASAN:
Dari gambar dapat kita lohat bahwa yang diarsir adalah $\$(P\backslash cap\; Q)-R)\$$ dan ini ekuivalen dengan $P\cap Q \cap R^c$.

Pilihan jawabannya adalah (A)

Soal 6: UMPTN 1998 Rayon B 
Jika $75$ siswa kelas III suatu SMU mengikuti UMPTN sebagai calon mahasiswa Perguruan Tinggi Negeri melakukan pilihan sebagai berikut:

• $30$siswa memilih sebagai calon mahasiswa ITB,
• 45 siswa memilih sebagai calon mahasiswa ITS,
• 20 siswa tidak memilih ITB maupun ITS,

maka siswa yang memilih sebagi calon mahasiswa kedua perguruan tinggi (ITB dan ITS) tesebut adalah...
(A) $10$
(B) $15$
(C) $20$
(D) $25$
(E) $30$

PEMBAHASAN:
$75$ siswa adalah seluruh peserta UMPTN yang memilih ITB, ITS, yang memilih keduanya atau yang tidak memilih keduanya.

Jika siswa yang memilih ITB kita misalkan $A$, yang memilih ITS kita misalkan $B$, dan yang tidak memilih keduanya $20$ maka dapat kita tuliskan:

$\begin{aligned}n(A \cup B)-20&=n(A)+n(B)-n(A \cap B)\\75-20&=  30+45-n(A \cap B)\\n(A \cap B)&=75-55\\&=20\end{aligned}$

Pilihan jawabannya adalah (C) 

Soal 7: UMPTN 1998 Rayon A 
Jika $50$ pengikut tes masuk suatu perguruan tinggi ada $35$ calon lulus Matematika, $20$ calon lulus Fisika, $10$ calon lulus Matematika dan Fisika, maka banyak calon pengikut yang tidak lulus kedua mata pelajaran itu ialah...
(A) $0$
(B) $5$
(C) $10$
(D) $15$
(E) $20$

PEMBAHASAN:
$50$ Peserta pengikut tes adalah seluruh peserta yang lulus fisika, matematika, yang lulus keduanya atau yang tidak lulus keduanya.

Jika pengikut tes lulus matematika kita misalkan $A$, pengikut tes lulus fisika kita misalkan $B$, dan mahasiswa yang tidak lulus keduanya $x$ maka dapat kita tuliskan:

$\begin{aligned}n(A \cup B)-x&=n(A)+n(B)-n(A \cap B)\\50-x&=  35+20-10\\n50-x&=40\\x&=5\end{aligned}$

Pilihan yang sesuai adalah (B)

Soal 7: UMPTN 1997 Rayon A,B,C 
Hasil pengamatan yang dilakukan terhadap $100$ keluarga menyatakan bahwa ada $55$ keluarga memiliki sepeda motor dan $35$ keluarga memiliki mobil. Jika ternyata ada $30$ keluarga yang tidak memiliki sepeda motor maupun mobil, maka banyaknya keluarga yang memiliki sepeda motor dan mobil adalah...
(A) $15$
(B) $20$
(C) $35$
(D) $45$
(E) $70$

PEMBAHASAN:
$100$ keluarga yang diamati adalah seluruh keluarga yang memiliki sepeda motor, mobil, yang punya keduanya atau yang tidak punya keduanya.

Jika keluarga yang punya sepeda motor kita misalkan $A$ dan keluarga yang punya mobil $B$, maka dapat kita tuliskan:

$\begin{aligned}n(A \cup B)-30&=n(A)+n(B)-n(A \cap B)\\100-30&=  55+35-n(A \cap B)\\n(A \cap B)&=90-70\\&=20\end{aligned}$

Pilihan jawabannya adalah (B)

Soal 8: UMPTN 1993 Rayon C 
Suatu survei yang dilakukan terhadap $100$ orang mahasiswa baru di suatu perguruan tinggi menyatakan bahwa $60$ orang mahasiswa memiliki mobil dan $25$ orang mahasiswa memiliki sepeda motor. Jika ternyata $30$ orang yang tidak memiliki mobil maupun sepeda motor, maka yang memiliki mobil dan sepeda motor adalah....
(A) $70$
(B) $45$
(C) $25$
(D) $15$
(E) $10$

PEMBAHASAN:
$100$ mahasiswa yang disurvei adalah adalah seluruh mahasiswa yang memiliki mobil, sepeda motor, yang memiliki keduanya atau yang tidak memiliki keduanya.

Jika mahasiswa yang memiliki mobil kita misalkan $A$, dan yang memiliki sepeda motor $B$, maka dapat kita tuliskan:

$\begin{aligned}n(A \cup B)-30&=n(A)+n(B)-n(A \cap B)\\100-30&=  60+25-n(A \cap B)\\n(A \cap B)&=85-70\\&=15\end{aligned}$

Pilihan jawabannya adalah (D)

Soal 9: UMPTN 1994 Rayon B 
Seratus orang pemuda mendaftarkan untuk mengikuti perlombaan jalan cepat, sepeda lambat, atau kedua-duanya. Bila yang mendaftarkan diri untuk mengikuti jalan cepat $75\%$, dan sepeda lambat $48\%$, banyaknya pemuda yang mendaftar untuk kedua lomba tersebut adalah...
(A) $22$
(B) $23$
(C) $32$
(D) $33$
(E) $48$

PEMBAHASAN:
Seratus orang pemuda adalah seluruh peserta yang ikut jalan cepat, sepeda lambat atau yang ikut keduanya.

Jika peserta yang mengikuti perlombaan jalan cepat kita misalkan $A$, dan yang mengikuti sepeda lambat $B$, maka dapat kita tuliskan:

$\begin{aligned}n(A \cup B)&=n(A)+n(B)-n(A \cap B)\\100&= 75+48-n(A \cap B)\\n(A \cap B)&=123-100\\&=23\end{aligned}$

Banyak peserta yang mengikuti perlombaan jalan cepat dan jalan cepat adalah $ 23$

Pilihan jawabannya adalah (B)

Soal 10: UMPTN 1994 Rayon B 
Suatu kompleks perumahan mempunyai 43 orang warga, 35 orang diantaranya aktif mengikuti kegiatan olahraga, sedang sisanya tidak mengikuti kegiatan apapun. Kegiatan bola voli diikuti 17 orang, tenis diikuti 19 orang, dan catur diikuti 22 orang. Warga yang mengikuti bola voli dan catur 12 orang, bola voli dan tenis 7 orang, sedang tenis dan catur 9 orang. Banyaknya warga yang mengikuti kegiatan bola voli, tenis dan catur adalah . . . .
(A) $5 \ orang \ $
(B) $7 \ orang \ $
(C) $17 \ orang \ $
(D) $20 \ orang \ $
(E) $28 \ orang \ $

PEMBAHASAN:
Misalkan:
S = himpunan warga kompleks
V = himpunan warga yang mengikuti kegiatan bola voli
C = himpunan warga yang mengikuti kegiatan catur
T = himpunan warga yang mengikuti kegiatan tenis

Dari soal diketahui:
$n(S)=43$; $n(V)=17$; $n(T)=19$, $n(C)=22$; $n(V \cup T \cup C)=35$; $n(V \cap C)=12$; $n(T \cap T)=7$; dan $n(T \cap C)=9$.

Kita gunakan:
$n(V \cup T \cup C)=n(V)+n(T)+n(C)-n(V \cap T)-n(V \cap C)$
                                 $-n(C \cap T)+ n(V \cap C \cap T)$

$\begin{aligned}35&=17+19+22-7-12-9+n(V \cap C \cap T)\\35 &= 58-28-n(V \cap C \cap T)\\35&=30-n(V \cap C \cap T)\\n(V \cap C \cap T)&=35-30 \\n(V \cap C \cap T)&=5\end{aligned}$

Pilihan jawabannya adalah (A)