Statistik Lima Serangkai
Dari suatu data dapat ditentukan lima buah nilai, yaitu datum terkecil xmin , datum terbesar xmaks , kuartil bawah Q1 , kuartil tengah Q2 , dan kuartil atas Q3 yang dianggap dapat memberikan gambaran mengenai tendensi sentral atau kecenderungan pemusatan dari data tersebut.
Kelima buah nilai itu dinamakan statistic lima serangkai. Dalam bentuk bagan, statistic lima serangkai diperlihatkan pada bagan di bawah ini
Langkah-langkah yang ditempuh untuk menentukan statistic lima serangkai dari suatu data adalah sebagai berikut :
- Buatlah statistik jajaran (peringkat) dari data itu, dengan cara mengurutkan nilai-nilai data itu dari yang terkecil sampai yang terbesar. Misalnya statistik jajarannya: x1 , x2 , x3 , x4 , . . ., xn . Nilai datum terkecil (dinamakan statistik minimum) adalah xmin = x1 dan nilai datum terbesar (dinamakan statistik maksimum) adalah xmaks = xn .
- Tentukan kuartil bawah Q1 , kuartil tengah Q2 , dan kuartil atas Q3 dari statistic jajarannya.
- Setelah nilai-nilai xmin , xmaks, Q1 , Q2 , dan Q3 diperoleh , sajikan statistic lima serangkai itu dalam bentuk bagan.
Kuartil bawah: $Q_{1}=x_{\frac{1}{4}(n+1)}=x_{\frac{1}{4}(15+1)}=x_{4}=7$
Kuartil tengah:
$Q_{2}=\frac{1}{2}(n+1)=x_{\frac{1}{2}(15+1)}=x_{8}=8$
Kuartil atas:
$Q_{3}=\frac{3}{4}(n+1)=x_{\frac{3}{4}(5+1)}=x_{12}=9$
Jadi, statistik lima serangkainya adalah
xmin = 2 dan xmaks = 10, Q1 = 7, Q2 = 8, dan Q3 = 9.
Bagan statistik lima serangkai disajikan sebagai berikut:
b. Rataan-kuartilnya:Rataan kuartil:
$R_{k}=\frac{1}{2}(Q_1 + Q_3)$
$R_{k}=\frac{1}{2}(7 + 9)=8$
Rataan tiga kuartil:
$R_{t}=\frac{1}{4}(Q_1 + 2Q_2 + Q_3)$
$R_{t}=\frac{1}{4}(7 + 2 \times 8 + 9)=8$
Contoh Soal 2
Panjang 40 ekor ikan (dalam cm) disajikan pada tabel distribusi frekuensi berikut ini.
|
Panjang (cm) |
48 |
50 |
51 |
53 |
54 |
55 |
57 |
58 |
|
Frekuensi (f) |
3 |
5 |
2 |
4 |
4 |
6 |
7 |
9 |
Tentukan statistik lima serangkainya!
Solusi:
ukuran data, n = 40
xmin = 48 dan xmaks = 58
Kuartil bawah:
$Q_{1}=x_{\frac{1}{4}(n+2)}=x_{\frac{1}{4}(40+2)}$
$Q_{1}=x_{10}+x_{\frac{1}{2}(x_{11}-x_{10})}$
$Q_{1}=51+x_{\frac{1}{2}(53-51)}=52$
Kuartil tengah:
$Q_{2}=\frac{1}{2}(x_{\frac{n}{2}}+x_{\frac{n}{2}+1})$
$Q_{2}=\frac{1}{2}(x_{20}+x_{21})$
$Q_{2}=\frac{1}{2}(55+55)=55$
Kuartil atas:
$Q_{3}=\frac{1}{4}(3n+2)=x_{\frac{1}{4}(120+2)}$
$Q_{3}=x_{30} + \frac{1}{2}(x_{31}-x_{30})$
$Q_{3}=57 + \frac{1}{2}(57-57)=57$
Jadi, statistik lima serangkainya adalah
xmin = 48 dan xmaks = 58, Q1 = 52, Q2 = 55, dan Q3 = 57.
Bagan statistik lima serangkai disajikan sebagai berikut:

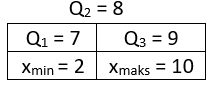

Post a Comment for "Statistik Lima Serangkai-Soal dan Pembahasannya"
Sobat Ayo Sekolah Matematika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!